cardinality

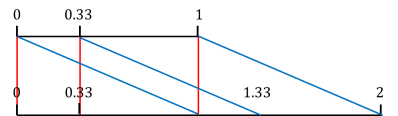
Continuing where I left off in the previous blog post: to prove that the set of infinite numbers between $0$ and $1$ is equal to the set of infinite numbers between $0$ and $2$ (assuming we are dealing with real numbers), we need a bijection between the two sets i.e. each number in one set must be paired uniquely to another number in the other set, and no numbers can be left over. This is simple: pair each $x$ in the set between $0$ and $1$ to $2x$ in the set between $0$ and $2$ .

Consider the above picture: if the top number line is the set of infinite numbers between $0$ and $1$ and the bottom is that between $0$ and $2$ , each line passes through a unique pair, and in this way, there are no numbers left that are unpaired in either set!

So we have proven that the two sets have the same cardinality – but isn’t this a bit paradoxical? How come the two sets are the same size, even though one wholly includes the other?

What if I joined each $x$ in the set between $0$ and $1$ to $x$ and $x + 1$ in the set between $0$ and $2$ ? Then wouldn’t the second set be twice as big as the first?

Or what if I joined each $x$ in the set between $0$ and $2$ to $\frac{x}{4}$ and $\frac{x}{4} + \frac{1}{2}$ – would the opposite would be true? Could a set be bigger than another set that includes it?

(I must admit, this is where my memory of Cantor’s set theory started to get a little hazy. I had to do a little research for this part…)

To answer the question, first off: “cardinality” is a little different from what the everyday definition of “size” is. As shown above, there are many arguments to show that one set could be bigger than the other. To bypass this, two sets are said to have the same cardinality simply if there exists a bijection between them. That is, just the fact that it is possible to pair the numbers in the two sets means that they have the same cardinality. Weird, I know.

So then, going back to Hazel’s argument that “some infinities are bigger than other infinities,” when can a set have a cardinality bigger than that of another set? Well, there must exist an injective function (but not a bijective function) from one set to another.

English: if it is impossible to pair the numbers in the two sets without having some numbers left over, one set is bigger than the other. What does this mean? Well, an example is always best, and Cantor’s diagonal argument offers a beautiful proof of why the infinite set of real numbers is bigger than the infinite set of natural numbers; such a set is said to be uncountable since the set’s elements cannot be numbered from $1$ to infinity. You can read more about it on Wikipedia here.

In summary: No, Hazel, unfortunately your “infinity” with Augustus is just as big as any other couple’s “infinity.” Of course, the distance between the two bounds $0$ and $1$ is smaller than the distance between the two bounds $0$ and $2$ , but the “number” of numbers between the two bounds for each set are the same. So, of course, you could argue that you have less time with Augustus, but the same number of points in time with him as anyone else.

But I have a feeling you don’t want to include all that in your eulogy. No, that wouldn’t be very romantic at all. So maybe you’re better off omitting that argument in your eulogy…

And for your information, I do get invited to a lot of parties, thank you very much.

*Rant over*

So I recently read The Fault in Our Stars by John Green. Seeing all the hype, I wanted to see what was so great about this new young adult romance comedy novel about two pretentious teenagers with cancer (but wait, it’s only a “side effect of dying”) that fall in love. Although they claim to be different from all those other kids with cancer… really, they’re not. The book is distasteful, its depiction of cancer is horrible, and most despicable of all, it has (gasp) a mathematical fallacy.

I’m kidding. It was a good light read.

Except for that last part, I’m not kidding about that. One of the biggest things that bothered me enough to make me stop chuckling at these terrible (in a good way) jokes for a while was the use of the line, “Some infinities are bigger than other infinities.” First off, the line was introduced completely out of the blue because Green wanted to make the characters look smarter and more pretentious (this also happened with Maslow’s hierarchy of needs). But aside from that, Green seriously didn’t do his research on Cantor, which isn’t too impressive considering he used it extensively to make a point in one of the passages.

To sum up that part (spoiler alert!), Hazel is delivering a eulogy for Augustus, in which she claims that there an infinite set of numbers between $0$ and $1$ , but there is a bigger infinite set of numbers between $0$ and $2$ . She feels that her situation is like that – the “unbounded set” (yet another mathematical fallacy – it is a bounded set) of time she has with him, despite being smaller than normal, provides her with a “forever within the numbered days.”

That’s great, Hazel. And actually, that’s really cute, even touching. Except it’s wrong.

Cantor’s set theory, especially that involving cardinality (i.e. size) of sets, shows that, in fact, the infinite set of numbers between $0$ and $1$ and the infinite set of numbers between $0$ and $2$ are the same “size”. To expand on that, any two infinite sets of numbers have the same cardinality if there exists a bijection between them. What does this mean? To demonstrate, we use an example with two finite sets:

Say Alphonse, Bryan, and Charles want to ask Alicia, Betty, and Claire to prom. We know that there will be enough girls for the guys to each get one partner because there are three boys and three girls – but how can we know that without knowing how many elements there are in each set? (Remember, we’re dealing with infinite sets!) The simplest way would be to pair each guy with a girl, and if there are no guys or girls left over, then the two sets have the same number of people!

(Interestingly, I read somewhere that this method was used by farmers in the past when counting wasn’t invented: to ensure that they weren’t missing any animals when they brought them in during the night, they would tie each animal to a separate stake; if there was a stake with a missing animal, they would then know that they had fewer animals than they were supposed to!)

This post is getting a bit long – I’ll continue this blog post here…

The Number Ghost

A blog about anything math

The Fault in Our Math, Pt. 2

The Fault in Our Math